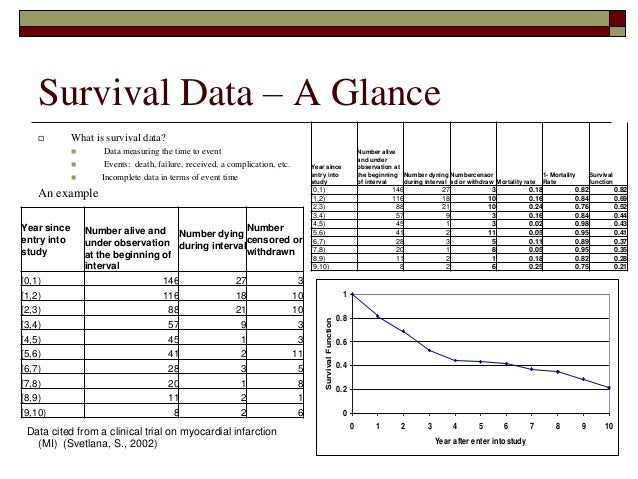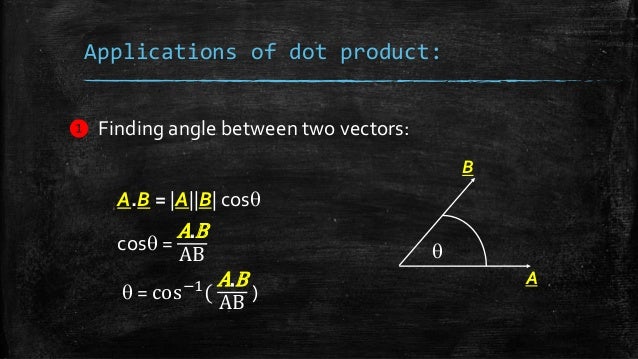
The Geometry of the Dot and Cross Products Free vector dot product calculator - Find vector dot product step-by-step
VECTORS Significance &application of Cross product
Dot Product Math is Fun. Dot and Cross Product October 31, 2007 - Happy Halloween! Dot Product (Inner product) Definition: Let a and b be two vectors in Rn, then the dot product of a and b, Dot Product vs Cross Product . Dot product and cross product are two mathematical operations used in vector algebra, which is a very important field in algebra. These concepts are widely used in fields such as electromagnetic field theory, quantum mechanics, classical mechanics, relativity and many other fields in physics and ….
- application of vectors to model and slove problems involving velocity and force - properties, computation and application of dot products of two vectors - properties, computation and application of cross products of two vectors - vector and scalar projections of vectors - cross product of two algebraic vectors in three-dimensional … Application to the law of cosines Edit There are two ternary operations involving dot product and cross product. The scalar triple product of three vectors is
VECTORS: Significance &Application of Cross product and Dot product. Cross product comes into picture whenever two objects work against each other, Vectors and the Dot Product The cross product is only de ned for three We can rewrite the equation j~v+ w~j 2= j~vj+ jw~j2 using dot products: (~v+ w
The Dot Product & The Cross Product. dot product, so does the cross product have One application of this result is a formula for the area Cross product tests for parallelism and Dot product tests for perpendicularity. Cross and Dot products are used in applications involving angles between vectors. For exa … mple given two vectors A and B; The parallel product is AxB=A||B|sin(AB). If AXB=|A||B|sin(AB)=0 then Angle (AB) is an even multiple of 90 degrees.
Cross and Dot products are used in applications involving angles between vectors. For example given two vectors A and B; The parallel product is AxB=AB|sin(AB). If AXB=|AB|sin(AB)=0 then Angle (AB) is an even multiple of 90 degrees. This is considered a parallel condition. Dot Product vs Cross Product . Dot product and cross product are two mathematical operations used in vector algebra, which is a very important field in algebra. These concepts are widely used in fields such as electromagnetic field theory, quantum mechanics, classical mechanics, relativity and many other fields in physics and …
Properties of the Cross Product, examples and solutions/ As with the dot product, the cross product of two vectors contains valuable Integral Applications. In mathematics, the cross product, vector product, or Gibbs' vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and therefore normal to the plane containing them.
3. a (b + c) = a b + a c. The cross product distributes across vector addition, just like the dot product. Likethedotproduct,thecrossproductbehavesalotlikeregularnumbermultiplication,withtheexception ofproperty1. Thecrossproductisnotcommutative. There are a lot of other algebraic … Vectors and dyadics • Dot product or cross product of a vector with a vector of application. 2.6 Vector addition
2017-12-12 · UNDERSTAND INTUITIVELY..... 1] How sin( ) is a measure of how much perpendicular two objects/forces are. 2] How cos( ) is a measure of how much parallel Vectors and dyadics • Dot product or cross product of a vector with a vector of application. 2.6 Vector addition
We give some of the basic properties of dot products and define orthogonal vectors and show how to use the dot product This application of the dot product A Practical Application of Vector Dot and Cross Products 129 Solar panels have to be installed carefully so that the tilt of the roof, and the direction to the sun, produce the largest possible electrical power in the solar panels. A simple application of vector dot and cross products lets us predict the amount of
Tutorial on the dot product of 2 vectors, examples with detailed solutions. 3. a (b + c) = a b + a c. The cross product distributes across vector addition, just like the dot product. Likethedotproduct,thecrossproductbehavesalotlikeregularnumbermultiplication,withtheexception ofproperty1. Thecrossproductisnotcommutative. There are a lot of other algebraic …
Time to make use of the dot product with this application. Learn about scalar projections, vector projections, and orthogonal projections in this math lesson. Writing the equation this way suggests a dot product: we can rewrite equation (2) to read Лќ 2 u u 3 v 2 v 3 Since the cross product of any two of these must have
The Dot and Cross Product LTCC Online. Understanding the Dot Product and the Cross Product Some Applications We used both the cross product and the dot product to prove a nice formula for the, 2017-12-12В В· UNDERSTAND INTUITIVELY..... 1] How sin( ) is a measure of how much perpendicular two objects/forces are. 2] How cos( ) is a measure of how much parallel.
Cross Product & Right Hand Rule Definition Formula

Cross product definition of Cross product and. Exercises: Dot Productand Cross Product This exercise explores the usage of dot product for calculation of projection lengths. Consider points P(1,2,3),A, For vectors and , the dot product is . The cross product is a vector orthogonal to three-dimensional vectors and , and can be used to determine the area or volume of a parallelogram defined by , , and . For vectors and , the cross product is , which is the determinate of a three-by-three matrix..
Dot Product Math is Fun
Cross Product & Right Hand Rule Definition Formula. Time to make use of the dot product with this application. Learn about scalar projections, vector projections, and orthogonal projections in this math lesson. https://en.wikipedia.org/wiki/Vector_algebra_relations Cross Product. A vector has magnitude (how long it is) and direction: Two vectors can be multiplied using the "Cross Product" (also see Dot Product) The Cross Product.

Free vector dot product calculator - Find vector dot product step-by-step - application of vectors to model and slove problems involving velocity and force - properties, computation and application of dot products of two vectors - properties, computation and application of cross products of two vectors - vector and scalar projections of vectors - cross product of two algebraic vectors in three-dimensional …
The dot product and cross product are methods of relating two vectors to one another. The dot product is a scalar representation of two vectors, and it is used to Introduction to the cross product with a The other multiplication is the dot product, as illustrated by these examples of calculating cross products and
2.5 Applications of Dot Products Example 1, page 3 of 3 We could have used the dot product to calculate directly, but to do so, we must define a new vector, a' a. Notice that the dot product of two vectors is a number and not a vector. For 3 dimensional vectors, we define the dot product similarly:
Calculus and Vectors – How to get an A+ 7.7 Applications of the Dot and Cross Product ©2010 Iulia & Teodoru Gugoiu - Page 2 of 2 C Parallelogram Area Vector Product of Vectors. The vector product and the scalar product are the two ways of multiplying vectors which see the most application in physics and astronomy.
Understanding the Dot Product and the Cross Product Some Applications We used both the cross product and the dot product to prove a nice formula for the The dot product and cross product are methods of relating two vectors to one another. The dot product is a scalar representation of two vectors, and it is used to
Dot and Cross Product Comparison/Intuition. If you're seeing this message, it means we're having trouble loading external resources on our website. DOT and CROSS PRODUCTS Both, however, have important applications to physics and the Dot Product, , quite frequently called the Inner
Calculus and Vectors – How to get an A+ 7.7 Applications of the Dot and Cross Product ©2010 Iulia & Teodoru Gugoiu - Page 1 of 2 7.7 Applications of the Dot and Calculus and Vectors – How to get an A+ 7.7 Applications of the Dot and Cross Product ©2010 Iulia & Teodoru Gugoiu - Page 2 of 2 C Parallelogram Area
You will also develop vector products and explore their applications. and describe applications of the dot product solve problems involving dot product and cross Application to the law of cosines Edit There are two ternary operations involving dot product and cross product. The scalar triple product of three vectors is
2017-12-12В В· UNDERSTAND INTUITIVELY..... 1] How sin( ) is a measure of how much perpendicular two objects/forces are. 2] How cos( ) is a measure of how much parallel VECTORS: Significance &application of Cross product and dot product. So the equation of friction will have i think cross-product and dot-product together.
2.5 Applications of Dot Products Example 1, page 3 of 3 We could have used the dot product to calculate directly, but to do so, we must define a new vector, a' a. View Notes - Dot Product, Cross Product and Applications from MTH 3030 at Baruch College, CUNY.
Introduction to the cross product. Vector dot and cross products. Vector dot product and vector length. Proving vector dot product properties. In mathematics, the cross product, vector product, or Gibbs' vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and therefore normal to the plane containing them.
Vectors and dyadics Stanford University

10Page129. The dot product of u and v is The cross product u v tells us the angle between u and v since 4. Another Application of the Cross Product:, View Notes - Dot Product, Cross Product and Applications from MTH 3030 at Baruch College, CUNY..
The cross product Math Insight
VECTORS Significance &application of Cross product. The Dot Product & The Cross Product. dot product, so does the cross product have One application of this result is a formula for the area, Vectors and dyadics • Dot product or cross product of a vector with a vector of application. 2.6 Vector addition.
The dot product and cross product are methods of relating two vectors to one another. The dot product is a scalar representation of two vectors, and it is used to Application Example 1 Problem: Dot products of unit vectors in spherical and rectangular Dot and Cross Product Author:
Free vector dot product calculator - Find vector dot product step-by-step We give some of the basic properties of dot products and define orthogonal vectors and show how to use the dot product This application of the dot product
Dot Product A vector has magnitude (how long it is) and direction: Here are two vectors: They can be multiplied using the "Dot Product" (also see Cross Product). - application of vectors to model and slove problems involving velocity and force - properties, computation and application of dot products of two vectors - properties, computation and application of cross products of two vectors - vector and scalar projections of vectors - cross product of two algebraic vectors in three-dimensional …
Calculus and Vectors – How to get an A+ 7.7 Applications of the Dot and Cross Product ©2010 Iulia & Teodoru Gugoiu - Page 2 of 2 C Parallelogram Area By this it gives a single number which indicates the component of a vector in the direction of another vector. Your observation of the dissimilarity between the dot and cross product is correct, however, the dot product is …
Cross Product. A vector has magnitude (how long it is) and direction: Two vectors can be multiplied using the "Cross Product" (also see Dot Product) The Cross Product The multiplication in vectors is defined in two ways: Dot product and cross product. The physical significance of both these is actually a beautiful concept. For
Cross product tests for parallelism and Dot product tests for perpendicularity. Cross and Dot products are used in applications involving angles between vectors. For exa … mple given two vectors A and B; The parallel product is AxB=A||B|sin(AB). If AXB=|A||B|sin(AB)=0 then Angle (AB) is an even multiple of 90 degrees. View Notes - Dot Product, Cross Product and Applications from MTH 3030 at Baruch College, CUNY.
Introduction to the cross product. Vector dot and cross products. Vector dot product and vector length. Proving vector dot product properties. Time to make use of the dot product with this application. Learn about scalar projections, vector projections, and orthogonal projections in this math lesson.
The simple takeaway: negative dot product means the vectors point in different directions. If the dot product is zero the two vectors are orthogonal (perpendicular). If the vectors are unit length and the result of the dot product is 1, the vectors are equal. Projecting Vectors. Say we want to know how much a vector is displacing in a certain … Examples of calculating the cross product. Skip to navigation (Press Enter) Skip to main content (Press The formula for the dot product in terms of vector components;
VECTORS: Significance &Application of Cross product and Dot product. Cross product comes into picture whenever two objects work against each other, For vectors and , the dot product is . The cross product is a vector orthogonal to three-dimensional vectors and , and can be used to determine the area or volume of a parallelogram defined by , , and . For vectors and , the cross product is , which is the determinate of a three-by-three matrix.
LG 8 – WORK – An Application of the Dot Product – SOLUTIONS. LG 9 – APPLICATIONS OF THE CROSS PRODUCT – Blank Copy. LG 9 Vectors. A vector is a quantity with a given magnitude and direction that connects the initial point A to the terminal point B, creating AB. (Links relevant to pages
Free Vector cross product calculator - Find vector cross product step-by-step 7.7 Applications of the Dot Product and Cross Product Physical Application of the Dot Product: When a force is acting on an object so that the object is moved from one
Applications of the Vector Dot Product for Game Programming. View Notes - Dot Product, Cross Product and Applications from MTH 3030 at Baruch College, CUNY., 2017-04-08В В· This video shows 3 examples of applications using the dot product and/or the cross product (torque, vector projection in 3-Space and volume of a.
Vectors and dyadics Stanford University

Vector Dot Product Calculator Symbolab. But I don't understand what do dot & cross products mean? What is the physical significance of dot & cross product of vectors? Web Applications;, Time to make use of the dot product with this application. Learn about scalar projections, vector projections, and orthogonal projections in this math lesson..
cochranmath / Vector applications of cross product and dot

Vectors and dyadics Stanford University. The dot product of u and v is The cross product u v tells us the angle between u and v since 4. Another Application of the Cross Product: https://en.wikipedia.org/wiki/Dot_product 1 The Dot and Cross Products Two common operations involving vectors are the dot product and the cross product. Let two vectors = , , and.

A Practical Application of Vector Dot and Cross Products 129 Solar panels have to be installed carefully so that the tilt of the roof, and the direction to the sun, produce the largest possible electrical power in the solar panels. A simple application of vector dot and cross products lets us predict the amount of But I don't understand what do dot & cross products mean? What is the physical significance of dot & cross product of vectors? Web Applications;
LG 8 – WORK – An Application of the Dot Product – SOLUTIONS. LG 9 – APPLICATIONS OF THE CROSS PRODUCT – Blank Copy. LG 9 The multiplication in vectors is defined in two ways: Dot product and cross product. The physical significance of both these is actually a beautiful concept. For
The cross product is a vector operation that acts on vectors in three dimensions and results in another vector in three dimensions. In contrast to dot product, which can be defined in both 2-d and 3-d space, the cross product is only defined in 3-d space. Cross Product. A vector has magnitude (how long it is) and direction: Two vectors can be multiplied using the "Cross Product" (also see Dot Product) The Cross Product
The dot product and cross product are methods of relating two vectors to one another. The dot product is a scalar representation of two vectors, and it is used to After watching this video lesson, you will be able to find the dot product of vectors both algebraically and geometrically. Learn the difference...
In mathematics and vector algebra, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ×. Cross product 5 wonderful Lagrange’s identity kxk2 kyk2 = (x†y)2 +kx£yk2: This identity relates norms, dot products, and cross products. In terms of the angle µ
Multiplying two vectors will sometimes give you another vector, known as a cross product, which has many important applications in the real world.... Multiplying two vectors will sometimes give you another vector, known as a cross product, which has many important applications in the real world....
Introduction to the cross product. Vector dot and cross products. Vector dot product and vector length. Proving vector dot product properties. 2017-04-08В В· This video shows 3 examples of applications using the dot product and/or the cross product (torque, vector projection in 3-Space and volume of a
Notice that the dot product of two vectors is a number and not a vector. For 3 dimensional vectors, we define the dot product similarly: 7.7 Applications of the Dot Product and Cross Product Physical Application of the Dot Product: When a force is acting on an object so that the object is moved from one
VECTORS: Significance &application of Cross product and dot product. So the equation of friction will have i think cross-product and dot-product together. In mathematics, the cross product, vector product, or Gibbs' vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and therefore normal to the plane containing them.
Exercises: Dot Productand Cross Product This exercise explores the usage of dot product for calculation of projection lengths. Consider points P(1,2,3),A The multiplication in vectors is defined in two ways: Dot product and cross product. The physical significance of both these is actually a beautiful concept. For
Calculus and Vectors – How to get an A+ 7.7 Applications of the Dot and Cross Product ©2010 Iulia & Teodoru Gugoiu - Page 2 of 2 C Parallelogram Area 2017-04-08 · This video shows 3 examples of applications using the dot product and/or the cross product (torque, vector projection in 3-Space and volume of a